OCP MX formats

OCP MX specification 문서

Preliminary

일상적으로 편하게 사용되는 floating point 의 구조:

• Sign bit, Exponent bits, Fraction bits 로 구성된다. Fraction 은 아래서 Mantissa 라고도 표기한다.

Single precision 의 경우 다음의 비트 구조를 가진다.

Single precision bit 구조 (from Wikipedia)

Exponent bits 에 따라 3개의 계산방법이 정해진다.

• Exponent = $00000000_2$ (Subnormal): $(-1)^{sign} \times 2^{-126} \times 0.\mathrm{fraction}$
• Exponent = $00000001_2 - 11111110_2$ (Normal): $(-1)^{sign} \times 2^{\mathrm{exponent}-127} \times 1.\mathrm{fraction}$
• Exponent = $11111111_2$: $\mathrm{fraction} = 0$ 이면 $\pm\infty$, $\mathrm{fraction} \ne 0$ 이면 $NaN$

Double precision 의 경우엔 다음의 비트 구조를 가진다.

Double precision bit 구조 (from Wikipedia)

Encoding 방식은 single precision 과 같다. Normal, Subnormal 이 구분되며, Exponent가 1로 가득찬 경우 Infinity 와 NaN 값만 표현된다.

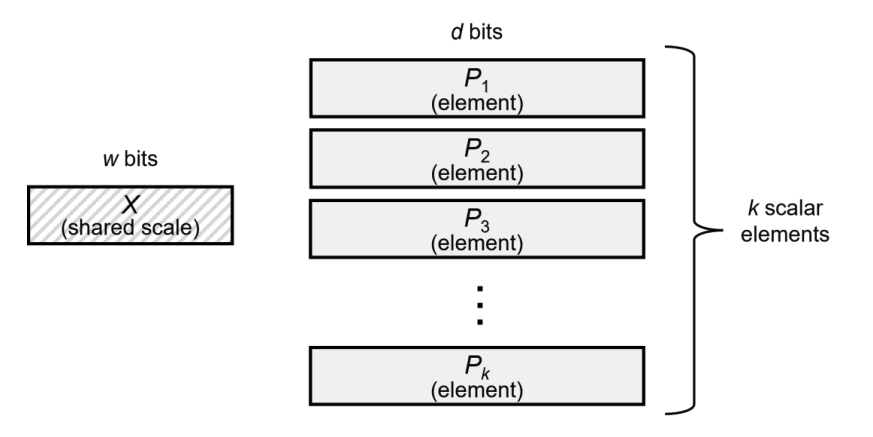
Microscaling (MX)

$k$ 개로 구성된 하나의 block 이 하나의 $X$ 라는 scale 값을 공유한다. 각 하나하나의 값 $v_{i}$ 는 다음의 규칙을 통해 정해진다.

• $X = \mathrm{NaN}$ 인 경우: $P_{i}$ 값에 무관하게 $v_{i}=\mathrm{NaN}$ 이 된다.
• $X \ne \mathrm{NaN}$ 인 경우:
  • $P_{i}$ 가 $\mathrm{NaN}$ 혹은 $\infty$ 라면, 그 값을 따른다.
  • $v_{i} = XP_{i}$ 가 float32 의 값 범위를 벗어나면 구현 방법에 따른다.
  • 그 외 $v_{i} = XP_{i}$

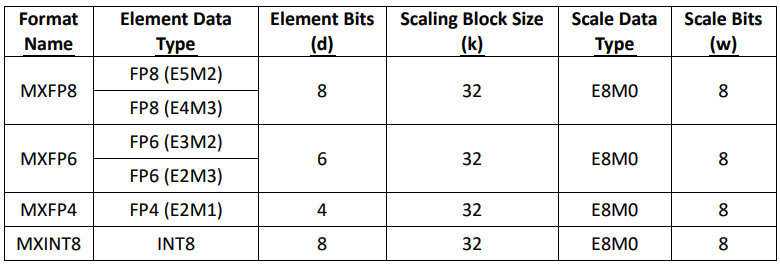
다양한 MX-compliant format 예제

FP8과 FP6 의 경우 Exponent 와 Mantissa 의 bit 수를 다르게 조정함으로써 가수 부분의 정밀도와 최대 표현 범위 사이의 trade-off 가 가능하게 하는 것을 볼 수 있다.

MXINT8 을 보면 가수부분을 날려버리고 전체 비트를 Exponent로 사용하게 되며 integer form 으로 돌아왔다. Integer 의 경우에도 block 단위로 scale 을 공유하게 한다면 bit 수를 아끼며 넓은 값 표현이 가능하게 된다.

각 FP 포맷마다 Normal, Subnormal, Infinity, NaN 을 구분하는 방식이 미묘하게 다르므로 자세한 것은 문서 참조.

MX format 의 dot product

$A$ 와 $B$ 라는 MX format 을 가지는 벡터가 있다:

\[A: \lbrace X^{(A)}, [P_{i}^{(A)}]^{k}_{i=1} \rbrace\] \[B: \lbrace X^{(B)}, [P_{i}^{(B)}]^{k}_{i=1} \rbrace\]

두 벡터를 내적한 스칼라 값 $C$ 는 다음과 같이 구해진다.

\[C = Dot(A, B) = X^{(A)}X^{(B)} \sum^{k}_{i=1}(P_{i}^{(A)} \times P_{i}^{(B)})\]

블록 벡터 내적 따로, scale X 값 곰셈을 따로 해도 되는 셈이다.

블록 여러개로 구성되는 긴 벡터의 경우에도 확장 가능하다. 이 때 각 block 을 구성하는 k 값은 같아야 하며, 두 벡터의 block 수는 같다고 가정한다. block 의 수는 패딩과 같은 방법을 통해 동일하게 달성될 수 있다.

\[C = DotGeneral(A, B) = \sum_{j=1}^{n}Dot(A_{j},B_{j})\]